据说数学是最纯粹的艺术，还在做数学考试噩梦的你知道吗？

保罗·洛克哈特

2020-01-14 17:32 来源：《一个数学家的叹息》

【编者按】
保罗·洛克哈特（Paul Lockhart），一位富有传奇色彩的数学家。大概14岁时，他对数学产生了浓厚兴趣（他特别指出，不是由于学校的数学课程）。为专心研究数学，他从大学退学，靠编程和当小学老师为生。1990年在哥伦比亚大学获得博士学位后，洛克哈特先后在加州大学伯克利分校的数学科学研究中心（MSRI）和布朗大学任职。2000年加入纽约的独立学校圣安学校，教导从幼儿园到12年级的数学课至今。保罗更愿意把数学看作一门艺术而不是科学，它是最纯粹的，能通过好奇、探索与游戏，打开孩子的心智，培养孩子的思维能力和艺术美感。在《一个数学家的叹息：如何让孩子好奇、想学习、走进美丽的数学世界》一书中，他澄清了数学教育的误区，展现了数学的艺术之美。本文摘编自该书的《数学与文化》一章，由澎湃新闻经青豆书坊授权发布。
首先我们要了解，数学是一门艺术。数学和其他类型的艺术（如音乐和绘画）的差别只在于，我们的文化不认同数学是一门艺术。每个人都了解，诗人、画家、音乐家创造出艺术作品，以文字、图像及声音来表达自我。事实上，我们的社会对创造性的表达是相当大方的，建筑师、厨师、甚至电视导播都被认为是职业上的艺术家。那么，为何数学家不是呢？这个问题，有一部分原因出在没有人知道数学家到底在做些什么。社会上的普遍认知似乎是，数学家和科学是有关联的——也许是因为数学家提供给科学家一些公式和定理，或者协助将一大堆数字输入计算机。如果这个世界必须要分成“诗意梦想家”和“理性思考家”两类人，毫无疑问，绝大多数人会把数学家放在后面那一类。
然而，事实上，没有什么像数学那样梦幻及富有诗意，那样激进、具破坏力和带有奇幻色彩。我们觉得天文学或物理学很震撼人心，在这一点上，数学完全一样（在天文学家发现黑洞之前，数学家老早就有黑洞的构想了），而且数学比诗、美术或音乐容许更多的表现自由，后者高度依赖这个世界的物理性质。数学是最纯粹的艺术，同时也最容易受到误解。
因此，让我试着解释数学是什么，以及数学家做些什么。我以英国数学家哈代（G.H.Hardy）绝佳的叙述作为开场：
一位数学家，就像一位画家或诗人，是模式（pattern）的创造者。如果他的模式比画家或诗人的模式能留存得更久，那是因为这些模式是用理念（ideas）创造出来的。
所以数学家的工作是做出理念的模式（making patterns of ideas）。什么样的模式？什么样的理念？是关于犀牛的理念吗？不是的，那些留给生物学家吧。是关于语言和文化的理念吗？不，通常不是。这些对大部分数学家的审美观而言，都太复杂了。如果数学有一个统一的美学原则的话，那将是：简单就是美（simple is beautiful）。数学家喜欢思考最简单的可能性，而这种最简单的可能性是想象的，不见得是现实存在的。
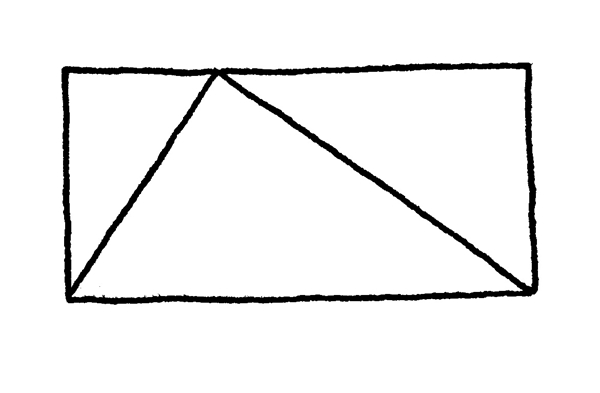
例如，如果现在我在思考形状——这是我常常做的——我可能会想象在长方形中有一个三角形：
我想知道，这个三角形占据了长方形多少的空间——三分之二吗？重点是要了解，我现在探讨的不是长方形内有三角形的这幅画；我探讨的，也不是组成桥梁上梁柱架构的那些金属三角形。在此，并没有那些深谋远虑的实用目的存在，我纯粹就是在玩。这就是数学——想知道（wondering）、游戏（playing）、用自己的想象力来娱乐（amusing）自己。首先，三角形在长方形中占据了多少空间，甚至没有任何真实、实体上的目的。即使是最谨慎小心制造出来的实体三角形，仍然是不断震动的原子所组成的，它的形状每分钟都在改变。也就是说，除非你要探讨“近似”（approximate）的度量。好了，这里就会牵扯到数学的“美学”了。因为那样就不单纯了，它成为一个依赖真实世界各式各样细节的丑陋问题了。那些留给科学家去解决吧。数学提出的问题是，在一个想象的长方形中有一个想象的三角形。它们的形状边缘很完美，因为我要它们很完美——这就是我喜欢思考的问题类型。这就是数学的一个主要特征：你想要它是什么样，它就是什么样。你有无限多的选项，没有真实世界来挡路。